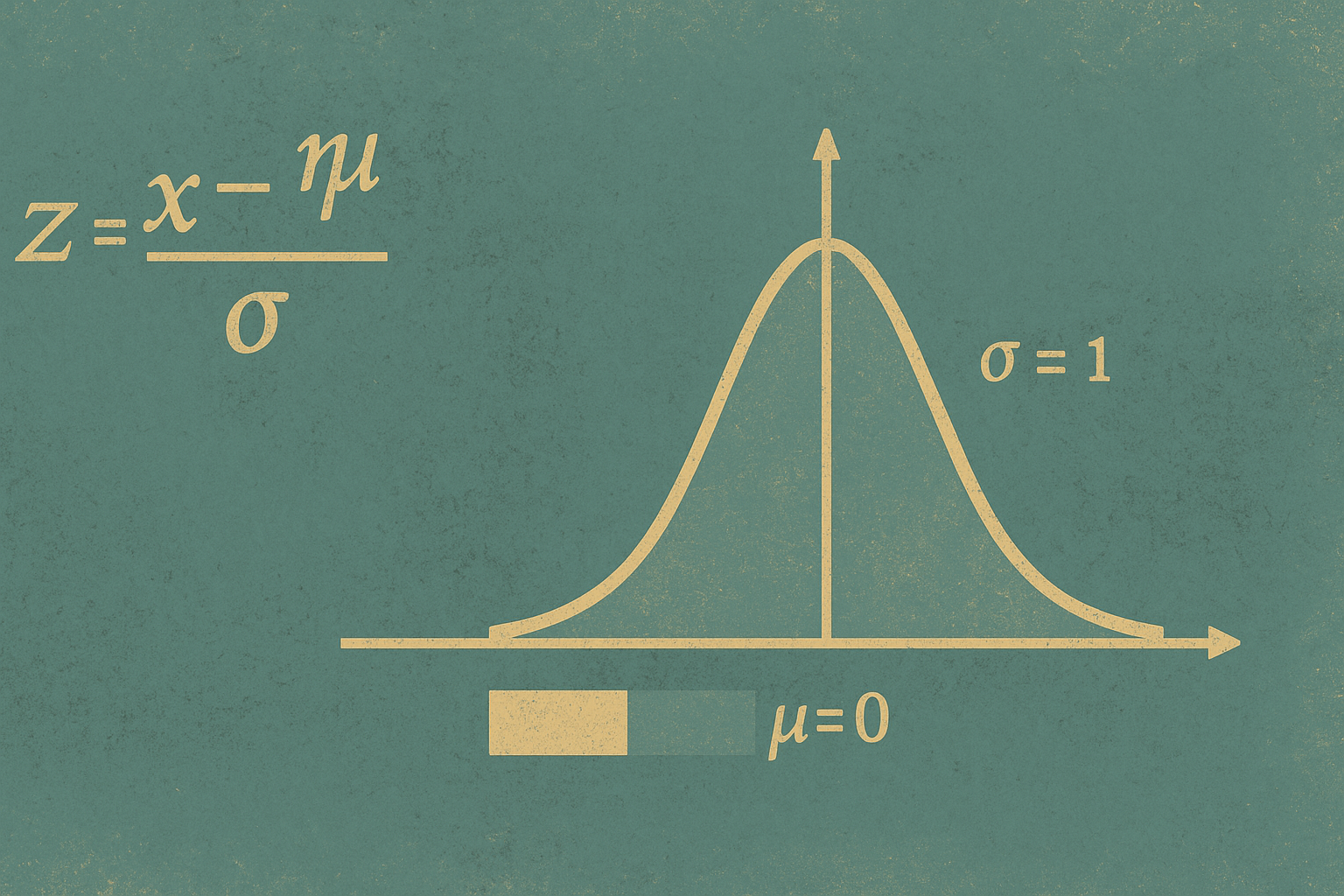Normalization vs Standardization - What to pick?

Have you ever trained a machine learning model and wondered why people keep talking about “scaling the data”?
Why does it matter if one feature is in the thousands while another is in decimals?

This is where Normalization and Standardization come in.
They’re not just math tricks — they’re ways to make sure your model doesn’t get biased by features with larger numbers. Think of them as putting all your features on the same playing field so models that rely on distances or gradients can learn fairly.

---

Why Scaling Matters

Imagine two features:

• Glucose: values around 3000
• GeneScore: values around 0.01

To a distance-based model, Glucose completely dominates. Scaling fixes this imbalance, letting models treat both features fairly.

---

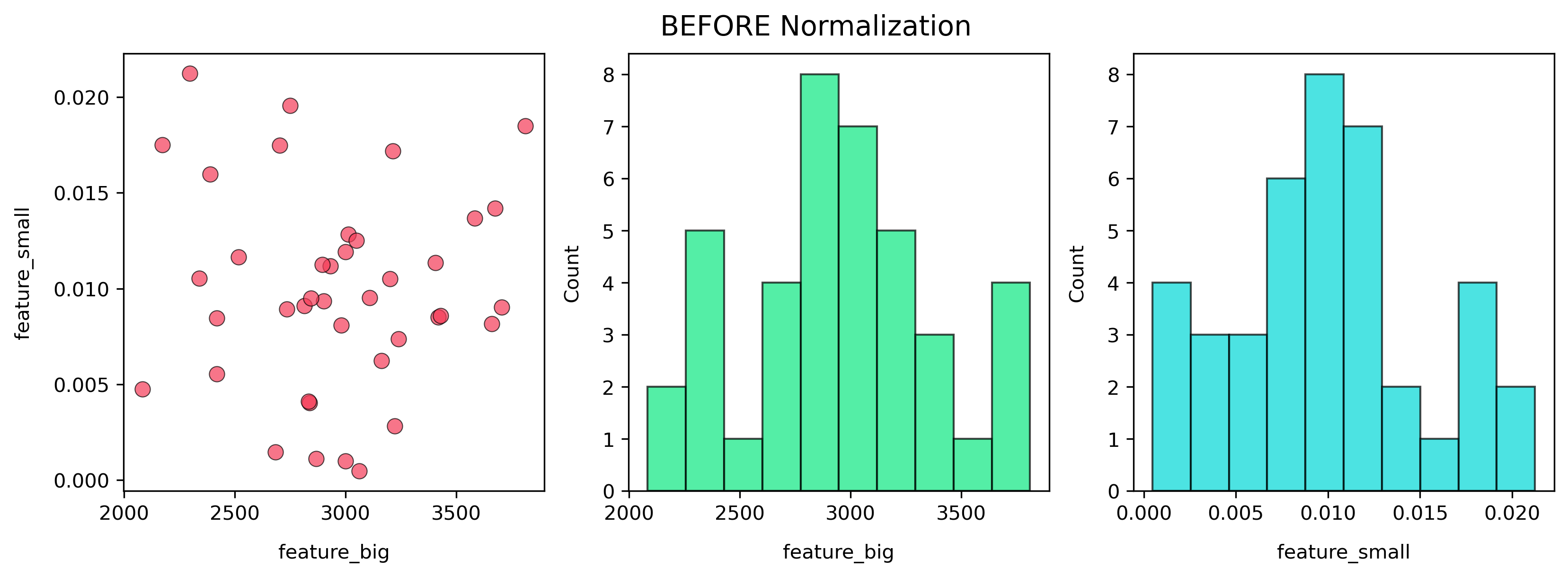
Before Scaling

Observation: x-axis spans thousands, y-axis hugs near zero. Without scaling, the smaller-scale feature is almost invisible to the model.

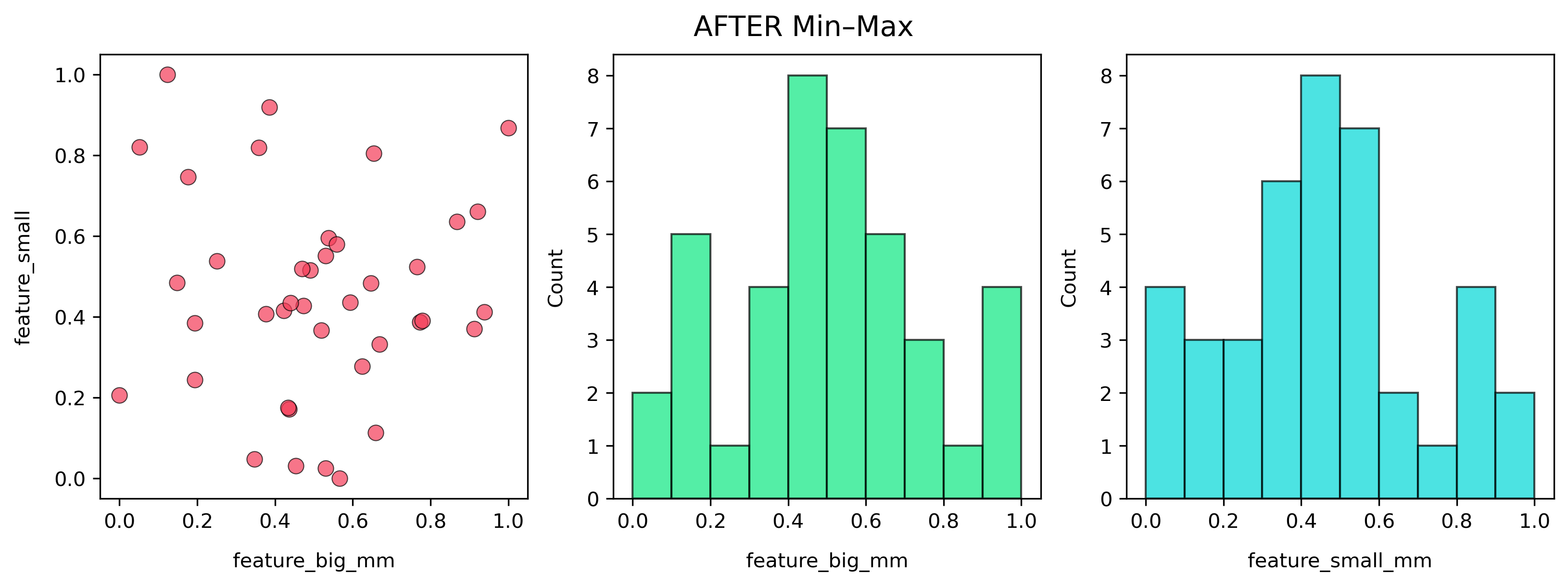
After Min–Max Normalization

Formula:

\[x_{norm} = \frac{x - x_{min}}{x_{max} - x_{min}}\]

Note: Both features now live between 0 and 1. The shapes are preserved, but the scale is uniform. A step of 0.1 means the same normalized change for both features.

---

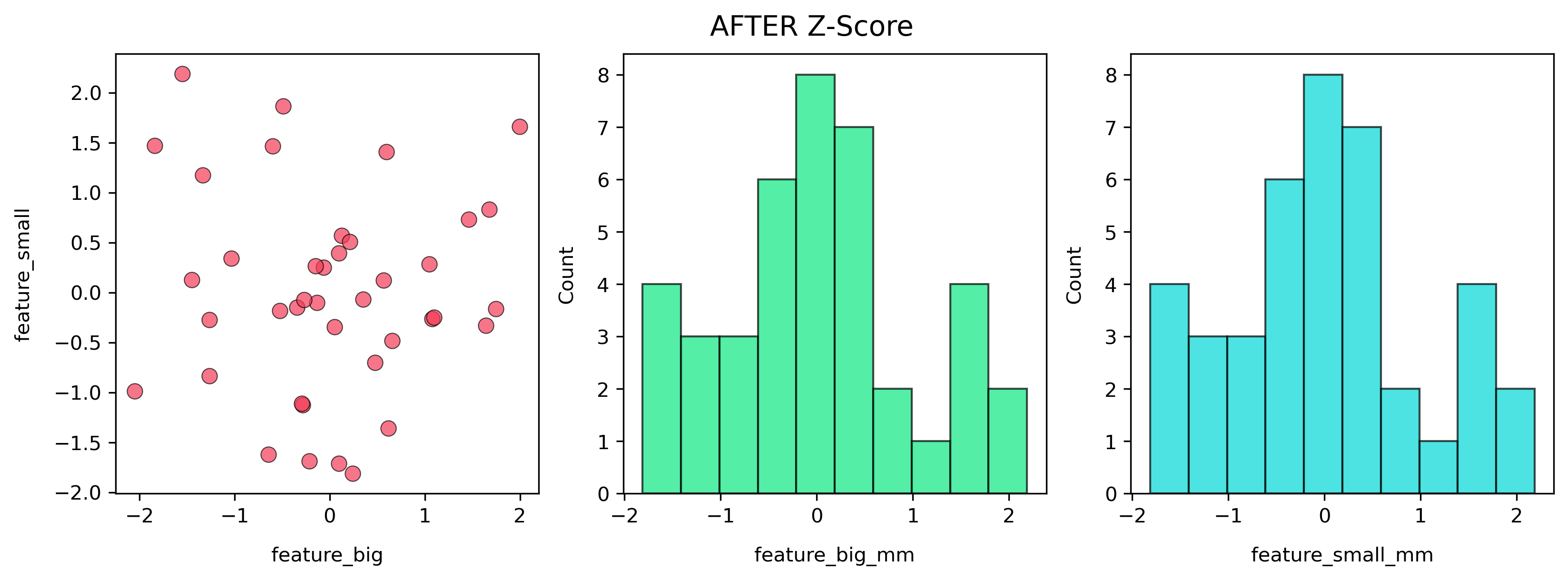
After Standardization (Z-score)

Formula:

\[z = \frac{x - \mu}{\sigma}\]

Note: Features are centered around 0 with similar spread (~1). Models like Logistic Regression, SVM, and many Neural Nets train more stably here.

---

When to Use What

• Normalization (Min–Max): when you want strict bounds [0, 1] or when the next step (like a neural net with sigmoid activations) expects inputs in that range.
• Standardization (Z-score): strong general default, especially for gradient-based models and PCA.
• No scaling needed: tree-based models (they split on thresholds, not distances).

---

Common Pitfalls

1. Data leakage: Always fit the scaler on training only, not the whole dataset.
2. Scaling categories: Don’t scale encoded categorical values (they aren’t “magnitudes”).
3. Outliers: Min–Max and Z-score can get distorted. (Outlier-robust scaling is a later topic.)

---

TL;DR (Cheat-Sheet)

• Normalization (Min–Max): squeezes values into a fixed range, usually [0, 1].
• Standardization (Z-score): shifts mean to 0 and scales spread to 1.
• Why scale? Puts features on a fair scale so distance- or gradient-based models don’t get biased by “big number” features.
• Use scaling for: kNN, SVM, Logistic/Linear Regression, Neural Nets, PCA, k-Means.
• Skip scaling for: Tree-based models (Decision Trees, Random Forests, XGBoost) — they don’t care about scale.

whenever magnitudes differ wildly and your model cares about distances or gradients.

Full notebook: GitHub

Happy scaling!