Cost Functions 101
Every deep learning model asks itself the same thing after making a prediction:
“How wrong am I right now?”
The answer comes from a cost function (also called a loss function).
It’s the model’s scoreboard of mistakes — telling it how far off it is, and how much it needs to adjust to get better.
In this post, we’ll look at three essential cost functions, in plain English and with a biology twist:
- Mean Squared Error (MSE)
- Hinge Loss
- Cross-Entropy
Mean Squared Error (MSE)
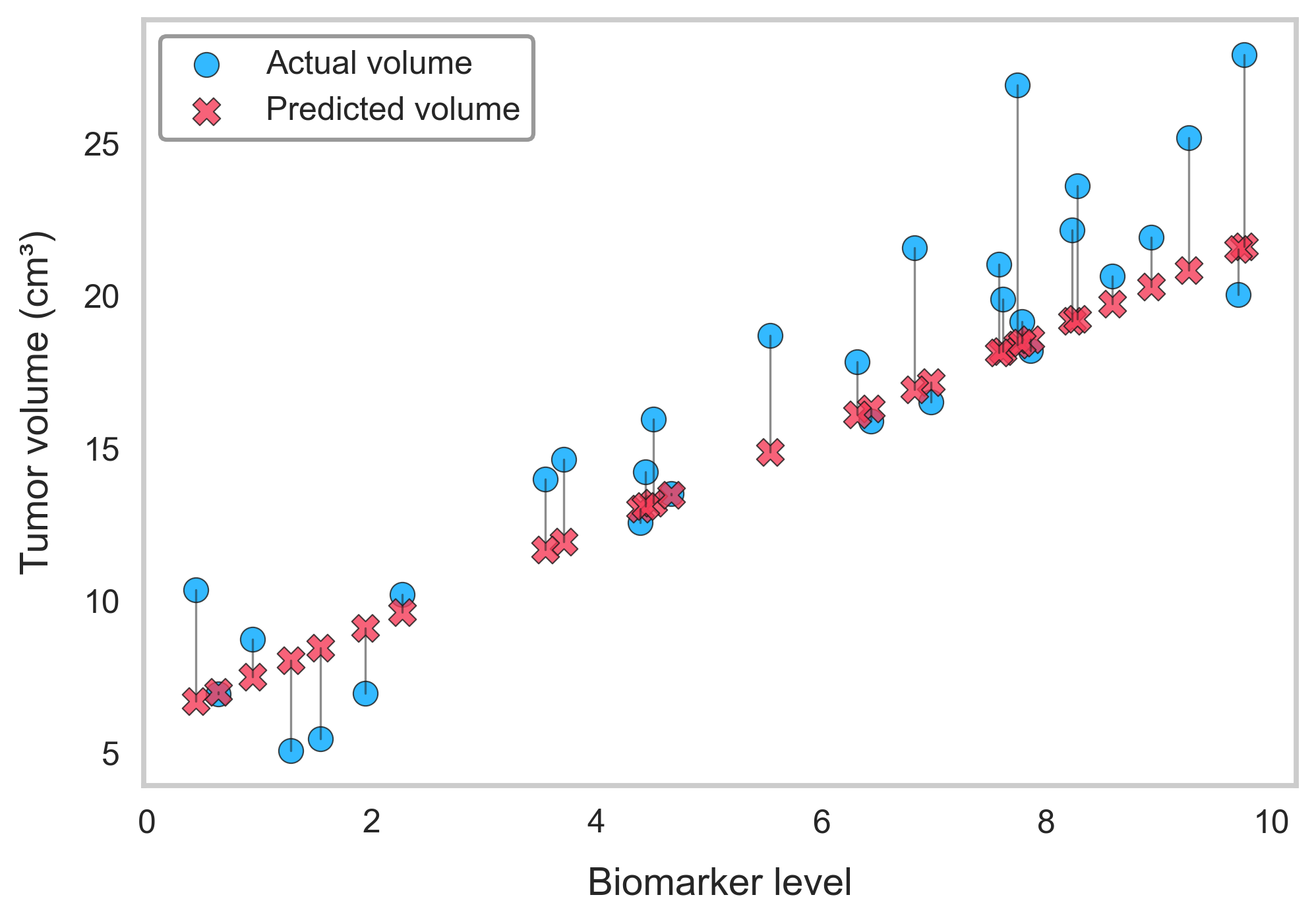
MSE is the most common cost function for regression problems — situations where we predict a continuous value, like tumor size, gene expression, or protein abundance.
It measures the average squared difference between predictions and true values:
\[\text{MSE} = \frac{1}{N} \sum_{i=1}^{N} \big( y_i - \hat{y}_i \big)^2\]In words:
- Find the difference between the true value ((y_i)) and predicted value ((\hat{y}_i)).
- Square the difference (so negatives don’t cancel out, and big mistakes hurt more).
- Average across all samples.
MSE is a perfectionist. Small mistakes don’t bother it much, but big errors get punished heavily.
Example:
If your model predicts a tumor volume of 3 cm³ when it’s actually 5 cm³, that’s an error of 2. Squared = 4.
But if it predicts 1 cm³ instead of 5 cm³, the error is 4. Squared = 16.
The second mistake looks 4x worse even though it’s only twice as far off.
Hinge Loss
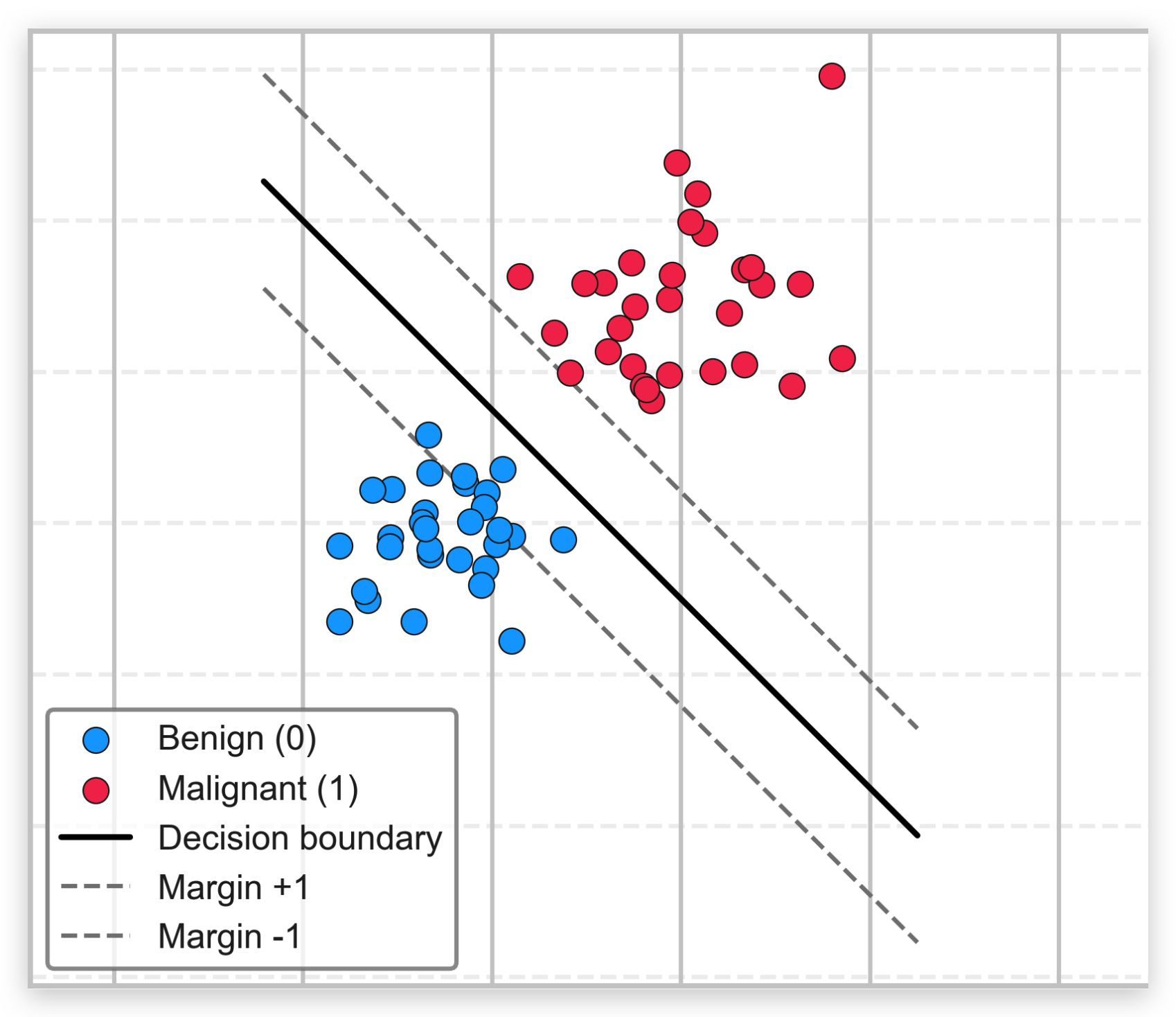
Hinge loss is popular in binary classification, especially with Support Vector Machines (SVMs).
It doesn’t just care about whether the prediction is right — it also checks if the model is confident enough.
The formula for one prediction is:
\[\text{Hinge}(y_i, f(x_i)) = \max \big( 0, \, 1 - y_i \cdot f(x_i) \big)\]and for the whole dataset:
\[L = \frac{1}{N} \sum_{i=1}^{N} \max \big( 0, \, 1 - y_i \cdot f(x_i) \big)\]- (y_i \in {-1, +1}) are the true labels (e.g., benign vs malignant).
- (f(x_i)) is the raw score from the model.
In words:
- If the model is right and confident → no loss.
- If it’s right but unsure (too close to the decision boundary) → small loss.
- If it’s wrong → big loss.
Think of hinge loss like a strict teacher. Even if you get the answer right, if you say it in a shaky voice, you still lose points.
Example:
In medical diagnosis, hinge loss encourages models to separate healthy vs cancer patients with a clear margin, not just a guess that’s barely correct.
Binary Cross-Entropy (Log Loss)
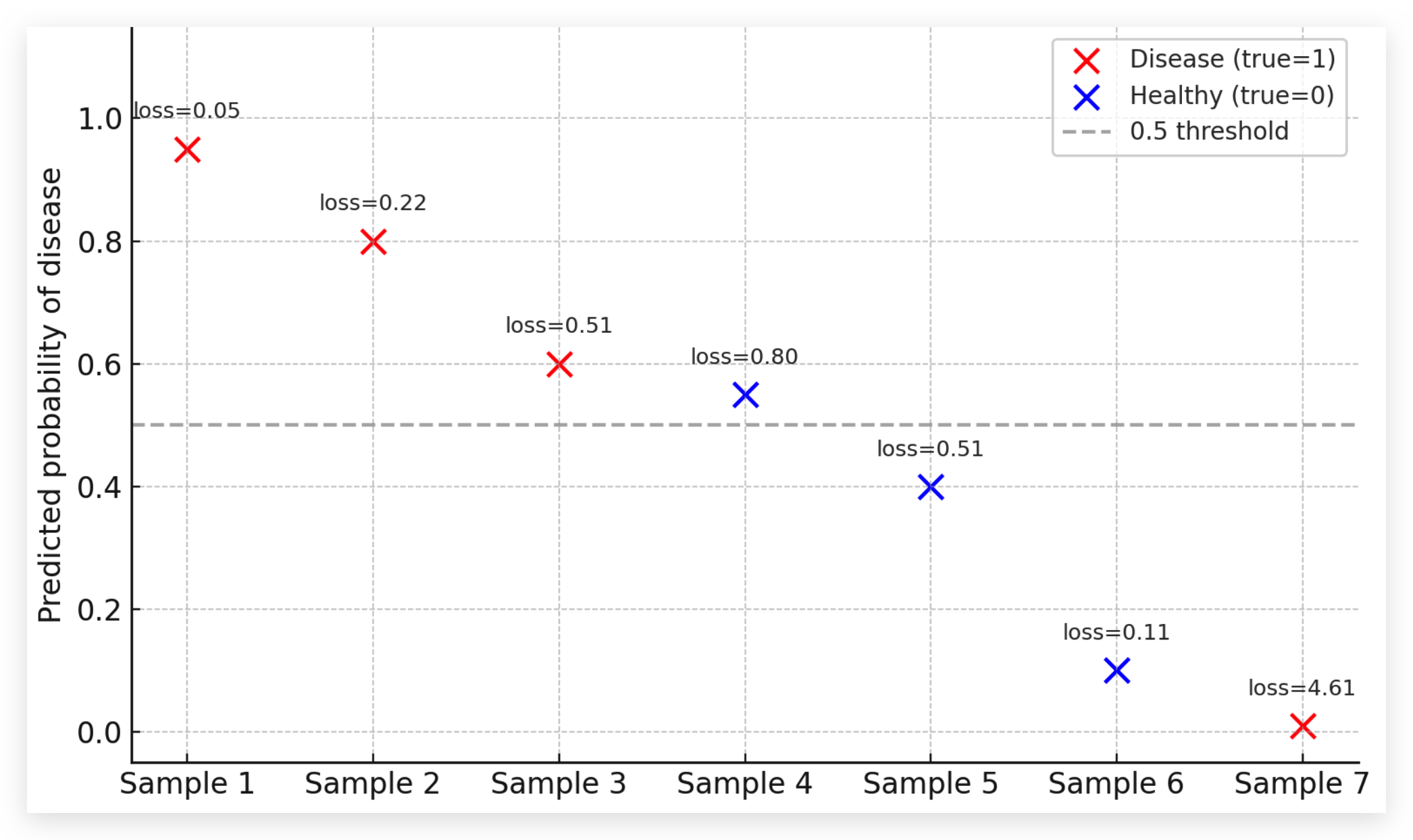
Cross-entropy is the superstar for classification problems.
Instead of just asking “right or wrong?”, it looks at the probabilities behind the prediction.
- (y_i \in {0,1}) = true label (e.g., 1 = disease, 0 = healthy).
- (\hat{p}_i) = predicted probability of class 1 (disease).
In words:
- Confident and correct → very small loss.
- Confident but wrong → huge loss.
- Uncertain predictions → medium loss.
Cross-entropy hates misplaced confidence. If your model is 99% sure a tumor is benign but it’s actually malignant — the penalty is enormous.
Example:
If your model predicts 95% cancer when the patient really has cancer → tiny loss (great!).
If it predicts 99% healthy when the patient has cancer → huge loss (disaster).
This makes cross-entropy ideal for tasks like disease subtype prediction, where both correctness and confidence matter.
Wrapping It Up
- MSE → Average of squared errors. Perfect for continuous predictions, punishes big mistakes harshly.
- Hinge Loss → Encourages clear, confident classification with margins. Great when you need separation.
- Cross-Entropy → Rewards correct confidence, punishes confident errors. Perfect for classification.
At the end of the day, cost functions are just different ways of saying “how wrong am I?”
They’re the compass that guides deep learning models through the training process, step by step, toward better predictions.
Think of cost functions as biology’s version of fitness landscapes. Just as evolution favors mutations that minimize survival cost, models evolve by minimizing error cost.
Full notebook: GitHub